Review I & II

Nama: Kenzie Castello Tiopan
NIM: 2301859051

Nama Dosen:
(Kelas Besar) Ferdinand Ariandy Luwinda (D4522) & Henry Chong (D4460)
(Kelas Kecil) Yovita Tunardi (D5025)

Review Semester II (First Half)

Linked List

Linked List (senarai berantai) adalah suatu struktur data linier yang dibentuk secara dinamik.

Terdapat tipe – tipe dari linked list, yaitu Single Linked List, Doubly Linked List, dan Circular Linked List.

• Singly Linked List

Singly linked list merupakan linked list yang memiliki 1 penghubung ke node lain. Setiap node memiliki data dan pointer ke node selanjutnya. Terdapat bagian awal yaitu head dan akhir yaitu tail dan tail memiliki pointer yang menunjukka NULL.

• Doubly Linked List

Doubly linked list merupakan linked list yang setiap nodenya memiliki 2 penghubung / pointer. 1 pointer menunjuk pada node selanjutnya dan 1 pointer lagi menunjuk pada node sebelumnya. Seperti gambar diatas terdapat node head yang pointer prevnya menunjuk NULL. Sama juga dengan tail.

• Circular Linked List

Sebenarnya terdapat 2 tipe circular linked list, yaitu circular singly linked list dan circular doubly linked list. Circular linked list sendiri merupakan variasi linked list yang akhir elemenya atau node tail berhubungan dengan node head sehingga menggambarkan suatu loop.

Method - Method pada linked list

• Push()

Push digunakan untuk menginsert value baru kepada suatu linked list. Dalam push dapat dilakukan dengan 3 cara yaitu pushHead, pushTail, dan pushMiddle. Contoh : Data = 1 2 3, jika dilakukan ingin mengisi 4 dengan pushHead data akan menjadi 4 1 2 3. Jika mengisi 4 dengan pushTail maka menjadi 1 2 3 4. Jika dilakukan pushMiddle 2.5 maka akann menjadi 1 2 2.5 3 4.
Contoh pengkodingan push head single linked list dan push head double linked list:
Push Head (SLL)

curr = newNode(value);

if(head == NULL)
head = tail = curr;
else
{
curr->next = head;
head = curr;
}

Push Head(DLL)
curr = (struct data*)malloc(sizeof(struct data));
curr->value = value;
curr->next = curr->prev = NULL;
if(head == NULL)
head = tail = curr;
else
{
curr->next = head;
head->prev = curr;
head = curr;
}

• Pop()

Pop digunakan untuk menghapus suatu value dari linked list. Contoh : Data = 1 2 3, jika dilakukan popHead dan popTail data akan menjadi 2.
Contoh pengkodingan pop head single linked list dan pop head double linked list:
Pop Head (SLL)
if(head == tail)
{
free(head);
head = tail = NULL;
}
else
{
curr = head;
head = head->next;
free(curr);

}

Pop Head (DLL)

curr = head;
if(tail == head)
{
tail = head = NULL;
free(curr);
}
else
{
head = head->next;
head->prev = NULL;
free(curr);
}

Untuk pengkodingan lebih mendetail pada push dan pop terhadap linked list terdapat pada link berikut

https://kctdatastructure.blogspot.com/2020/02/linked-list.html (Double Linked List)

https://kctdatastructure.blogspot.com/2020/03/linked-list-ii.html (Single Linked List)

Hashing Table & Binary Tree

• Hashing Table

Hash table adalah suatu data struktur yang menyimpan data secara teratur yang saling berhubungan. Pada sebuah hash table, data disimpan dalam bentuk array, dimana setiap value dari suatu data memiliki index value uniknya sendiri. Pengaksesan data menjadi lebih cepat jika kita mengetahui index dari data tersebut.

Hashing adalah teknik untuk mengconvert value key - key menjadi index - index array. Contohnya jika terdapat hash table dengan size 20 maka berlaku rumus H(x) = [ x % 20 ]. Jika list yang ingin diconvert adalah List = [ 21, 22, 23, 24, 25 ].

Maka pada hash table akan berisi seperti berikut :

Pada hashing table terdapat 2 metode yaitu insert dan delete. Contoh kodingan insert:

Insert

int idx = hashCode(id);  <Function ini untuk mengconvert value key menjadi index array>

curr = create(id, name);

if(head[idx] == NULL)

head[idx] = tail[idx] = curr;

else

{

curr->prev = tail[idx];

tail[idx]->next = curr;

tail[idx] = curr;

}

• Binary Tree

Binary tree adalah suatu data struktur yang digunakan untuk menyimpan data. Suatu binary tree memiliki kondisi dimana setiap node paling maksimum memiliki 2 anak.

Terdapat 3 jenis binary tree yaitu:

• Full Binary Tree:
  Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
• Complete Binary Tree:
  Mirip dengan Full Binary Tree, namun tiap subtree boleh memiliki panjang path yang berbeda. Node kecuali leaf memiliki 0 atau 2 child.
• Skewed Binary Tree:
  yakni Binary Tree yang semua nodenya (kecuali leaf) hanya memiliki satu child.

Untuk pengkodingan pada hashing table dapat dilihat pada link berikut:

https://kctdatastructure.blogspot.com/2020/03/hashing-table-binary-tree.html

Binary Search Tree

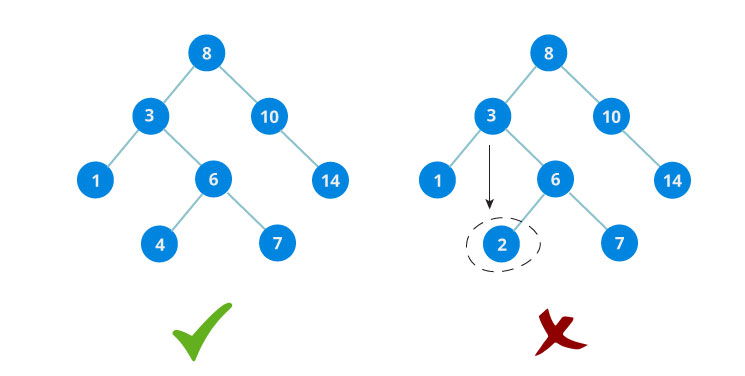
Binary search tree dpt dimengertikan sebagai sebuah struktur data yang dapat kita gunakan untuk mengurutkan angka - angka. BST juga dapat dimengertikan sebagai binary tree yang dimana setiap node hanya memiliki value terkecil pada subtree kiri dan value yang terbesar pada subtree kanan serta node dari kedua subtree juga merupakan BST. Contohnya seperti yang berikut ini :

Binary tree kanan salah dikarenakan node dengan value 3 lebih kecil dari pada node key utama.

Akan dikatakan sebagai binary tree jika setiap node dari tree memiliki maksmimal 2 anak. Akan dikatakan sebagai search tree jika tree tersebut dapat mencari value dari 0(log(n)) kali.

Terdapat 3 cara untuk melakukan penelusuran data (traversal) pada BST:

• PreOrder : Print data, telusur ke kiri, telusur ke kanan.
• InOrder : Telusur ke kiri, print data, telusur ke kanan.
• Post Order : Telusur ke kiri, telusur ke kanan, print data.

Pada BST juga terdapat 2 metode yaitu insertion dan deletion. 

• Insertion untuk menambah data pada binary tree
• Deletion untuk menghapus data dari binary tree dan biasanya terdapat 3 kemungkinan yang bisa terjadi, yaitu:
• Jika node yang dihapus adalah leaf (Langsung hapus dari tree).

• Jika node yang dihapus memiliki 1 anak (Copy anak tersebut pada node yang akan dihapus dan hapus nodeny)

• Jika node yang dihapus memiliki 2 anak (Cari inorder successor, yaitu value yang lebih besar daripada value node dan memiliki selisih paling kecil, lalu copy isi inorder successor pada node dan hapus node tersebut)

Untuk pengkodingan dan penjelasan lebih detail dapat dilihat melalui link ini:

https://kctdatastructure.blogspot.com/2020/03/binary-search-tree.html

Review Semester II (Second Half)

AVL Tree

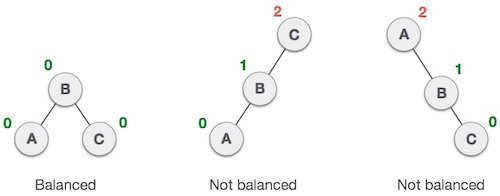
AVL Tree berasal dari nama penemunya yaitu Adelson, Velski & Landis, yang merupakan tree yag digunakan untuk membalance binary search tree. AVL tree mengecek ketinggian dari sub-tree / leaf kiri dan kanan dan memastikan bahwa perbedaan tinggi tidak lebih dari 1. Perbedaan ini disebut Balance Factor.

Pada tree kedua dikatakan tidak balance dikarenakan sub-tree kiri dari C itu 2 dan sub-tree kanannya adalah 0, jadi perbedaan tingginya adalah 2, maka melanggar syarat balance factor. Jika masalah seperti ini terjadi, maka AVL tree mempunyai beberapa teknik untuk menyelesaikan masalah tersebut yang dinamakan AVL Rotation. 

Contoh perbaikan dari no-AVL tree ke AVL tree :

Terdapat 2 kasus dalam insertion AVL balancing yang menyebabkan diperlukannya menggunakan salah satu teknik rotasi :

Insertion

1. Single Rotation

Jika node yang menyebabkan tidak balance itu berupa kiri - kiri

Jika dilihat dari gambar diatas, T1 menyebabkan pelanggaran balance factor terhadap node z dikarenakan selisih sub-tree kiri kanan dari z adalah 2, maka untuk memperbaikinya harus dilakukan penarikan z ke kanan dan T3 menjadi sub-tree z.

2. Double Rotation

Jika node yang menyebabkan tidak balance itu berupa kiri - kanan

Jika dilihat dari gambar diatas, T3 menyebabkan pelanggaran balance factor terhadap node z dikarenakan selisih sub-tree kiri dan kanan z adalah 2, maka untuk memperbaikinya harus dilakukan penarikan y ke kiri dan T2 menjadi sub-tree y. Dikarenakan masih belum balance pada node z dilakukan rotasi sekali lagi.

Deletion

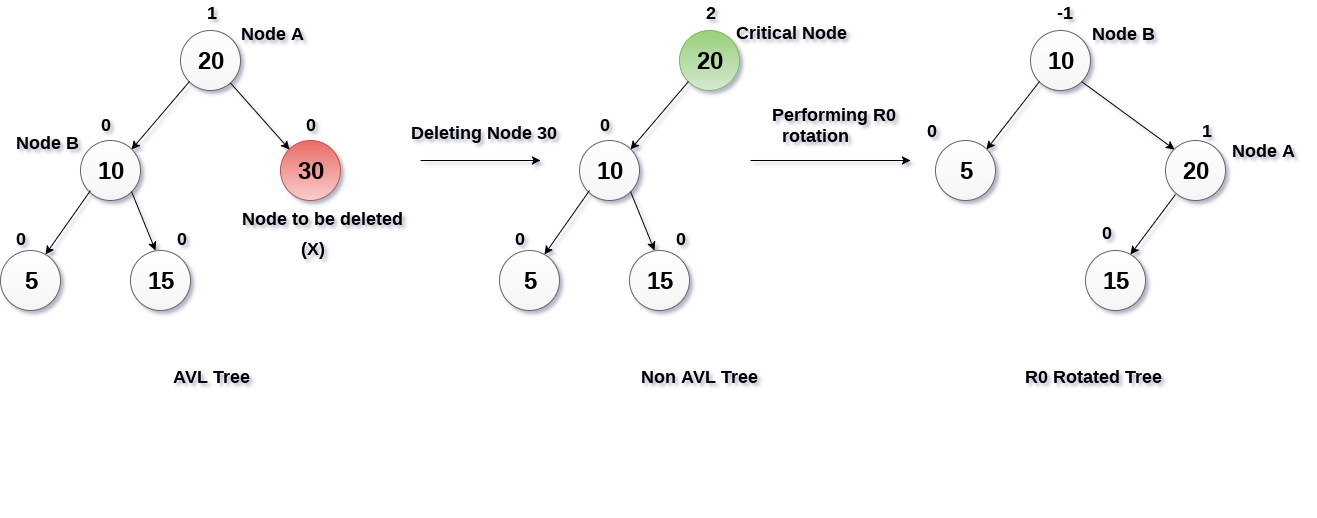
Terdapat 2 jenis kasus dalam penghapusan suatu node dalam AVL tree:

1. Jika node yang ingin dihapus merupakan node yang tidak memiliki sub-tree lalu dilakukan pengecekan kembali balance factor.

2. Jika node yang ingin dihapus memiliki sub-tree sehingga harus mencari successor atau predecessor untuk menggantikan node tersebut, lalu dilakukan pengecekan kembali balance factor.

Gambar diatas merupakan salah satu kasus yang dalam proses deletion pada suatu node yaitu kasus pertama. Maka node (30) langsung dihapus karena tidak terdapat sub-tree dan dilakukan pengecekan balance factor. Ternyata selisih sub-tree kiri dan kanan node (20) lebih dari satu. Maka node (20) ditarik ke kiri sehingga node (10) menjadi node paling awal dan node (15) berpindah menjadi sub-tree kiri node (15).

Reference ; https://algorithms.tutorialhorizon.com/avl-tree-insertion/

Heap

Heap merupakan suatu tree-based data structure yang dimana merupakan sebuah tree yang hampir komplit yang melengkapi syarat heap property (Setiap nodepada sebuah tree yang memiliki key yang lebih besar, lebih kecil, atau sama dengan key dari parentya). Terdapat cara penentuan parent dan child pada heap, yaitu sebagai berikut:

Misalkan x adalah suatu elemen (Angka merah menandakan array)

- Parent : x / 2, cth : 4 / 2 = 2

- Left Child : x * 2, cth : 4 * 2 = 8

- Right Child : (x * 2) + 1, cth : (4 * 2) + 1 = 8 + 1 = 9

Terdapat 2 macam heap yaitu Max heap dan Min heap.

• Max Heap : Pada max heap terdapat key yang berada pada root node yang harus lebih besar daripada key anak - anaknya.

 Jika dilakukan max heap insertion:
- Node baru akan diinsert pada array index selanjutnya (Pada contoh diatas left child dari node 10)
- Akan dibandingkan node yang baru dan value node diatasnya, bila lebih besar diswap (Dilakukan sampai value parent lebih besar

Jika dilakukan max heap deletion:
- Delete node yang ingin dihapus
- Node digantikan node yang berada di paling kanan bawah (Jika node yang dihapus memiliki left atau right child)
  - Jika heap property sudah benar maka selesai.
  - Jika value node pengganti >= node parentnya maka diswap, lalu diulang cek sampai heap property.
  - Jika tidak, tukar dengan node child paling besar.

• Min Heap : Pada min heap terdapat key yang berada pada root node yang harus merupakan nilai minimum diantara key anak - anaknya.

Min heap deletion dan insertion sama dengan max heap hanya lebih besar menjadi lebih kecil

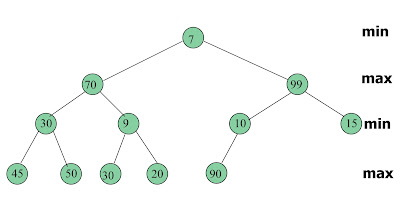
• Max-Min Heap : Merupakan binary tree komplit yang berisi level min (genap) dan max (ganjil) 

Jika dilakukan max-min heap insertion:

- Insert node baru pada index selanjutnya (Contoh diatas diinsert pada right child 10)

- Dilakukan proses heapify (Mengecek node yang baru dengan parentya dan grandparentnya sesuai dengan level)

- Proses dilakukan sampai heap property benar

Tries

Sebuah trie adalah tree mirip data structure yang menyimpan node huruf alfabet.

Insertion pada Trie
Semua karakter yang diinsert termasuk sebagai node trie individu. Children node merupakan suatu array of pointers terhadap trie node diatasnya. Karakter key merupakan index terhadap childrennya. Jika key yang diinput baru atau merupakan tambahan dari key yang sudah ada, maka diharuskan membuat node baru dari key tersebut dan tandai node selanjutnya sebagai EOW (End of Word).

Kata - kata yang terdapat pada gambar diatas adalah

- CAR

- CAB

- CAN

Aplikasi dari trie adalah

- Autocomplete 

- Search engine browser

- Bubble words