Binary Search Tree

Binary Search Tree

Binary search tree dpt dimengertikan sebagai sebuah struktur data yang dapat kita gunakan untuk mengurutkan angka - angka. BST juga dapat dimengertikan sebagai binary tree yang dimana setiap node hanya memiliki value terkecil pada subtree kiri dan value yang terbesar pada subtree kanan serta node dari kedua subtree juga merupakan BST. Contohnya seperti yang berikut ini :

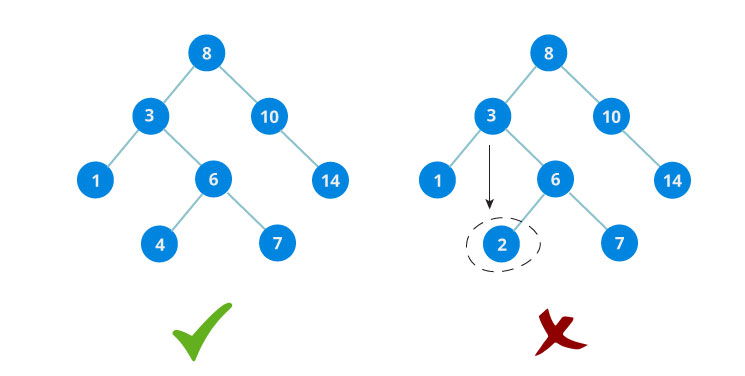
Binary tree kanan salah dikarenakan node dengan value 3 lebih kecil dari pada node key utama.

Akan dikatakan sebagai binary tree jika setiap node dari tree memiliki maksmimal 2 anak. Akan dikatakan sebagai search tree jika tree tersebut dapat mencari value dari 0(log(n)) kali.

Terdapat 2 operasi basic, yaitu insertion dan deletion :

Insertion

• Dimulai dari awal (root).
• Bandingkan value (x) yang ingin diinsert dengan root.
• Jika lebih kecil, maka cek x dengan subtree kiri dan lakukan secara berulang(rekursif).
• Jika lebih besar, maka cek x dengan subtree kanan dan lakukan secara berulang(rekursif). 
• Lakukan sampai ditemukan node yang kosong untuk dimasukkan value x (sebagai leaf).

Jika dilakukan insert node dengan value 40 akan menjadi :

Deletion

• Terdapat 3 kemungkinan dalam operasi deletion
• Jika node yang dihapus adalah leaf (Langsung hapus dari tree).

Jika dilakukan delete pada node 40 akan menjadi :

• Jika node yang dihapus memiliki 1 anak (Copy anak tersebut pada node yang akan dihapus dan hapus nodeny)

Jika dilakukan delete pada node 30 akan menjadi :

• Jika node yang dihapus memiliki 2 anak (Cari inorder successor, yaitu value yang lebih besar daripada value node dan memiliki selisih paling kecil, lalu copy isi inorder successor pada node dan hapus node tersebut)

Jika dilakukan delete pada node 20 akan menjadi :