Hashing Table
Hash table adalah suatu data struktur yang menyimpan data secara teratur yang saling berhubungan. Pada sebuah hash table, data disimpan dalam bentuk array, dimana setiap value dari suatu data memiliki index value uniknya sendiri. Pengaksesan data menjadi lebih cepat jika kita mengetahui index dari data tersebut.
Maka, akan menjadi sebuah data struktur yang dimana operasi insertion dan search menjadi lebih cepat walaupun data tersebut memiliki ukuran yang besar. Hash table memakai sebuah array sebagai storage dan memakai teknik hash untuk membuat sebuah index dimana suatu elemen diinsert atau dicari.
Hashing
Hashing adalah teknik untuk mengconvert value key - key menjadi index - index array. Contohnya jika terdapat hash table dengan size 20 maka berlaku rumus H(x) = [ x % 20 ]. Jika list yang ingin diconvert adalah List = [ 21, 22, 23, 24, 25 ].
Maka pada hash table akan berisi seperti berikut :
Contoh pengkodingan insert dan delete:
Insert
void insert(int key, int data) {
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
int hashIndex = hashCode(key);
while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
++hashIndex;
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
Delete
struct DataItem* delete(struct DataItem* item) {
int key = item->key;
int hashIndex = hashCode(key);
while(hashArray[hashIndex] != NULL) {
if(hashArray[hashIndex]->key == key) {
struct DataItem* temp = hashArray[hashIndex];
hashArray[hashIndex] = dummyItem;
return temp;
}
++hashIndex;
hashIndex %= SIZE;
}
return NULL;
}
Binary Tree
Binary tree adalah suatu data struktur yang digunakan untuk menyimpan data. Suatu binary tree memiliki kondisi dimana setiap node paling maksimum memiliki 2 anak.
Terdapat 3 jenis binary tree yaitu:
- Full Binary Tree:
Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
- Complete Binary Tree:
Mirip dengan Full Binary Tree, namun tiap subtree boleh memiliki panjang path yang berbeda. Node kecuali leaf memiliki 0 atau 2 child.
- Skewed Binary Tree:
yakni Binary Tree yang semua nodenya (kecuali leaf) hanya memiliki satu child.
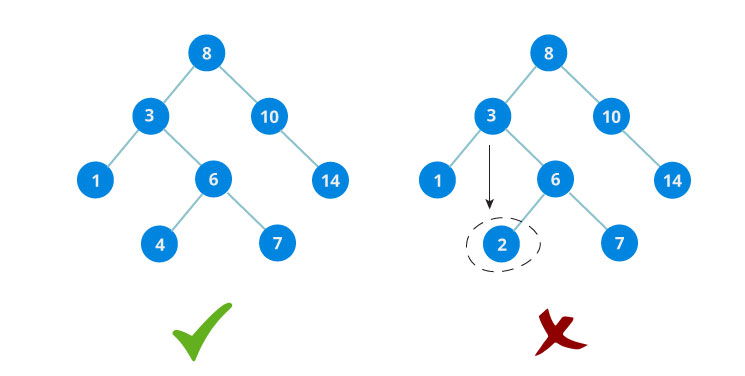
Binary Search Tree
Binary search tree adalah struktur data yang mengadopsi konsep Binary Tree namun terdapat aturan bahwa setiap clild node sebelah kiri selalu lebih kecil nilainya dari pada root node. Begitu pula sebaliknya, setiap child node sebelah kanan selalu lebih besar nilainya daripada root node.
Terdapat 3 cara untuk melakukan penelusuran data (traversal) pada BST:
- PreOrder : Print data, telusur ke kiri, telusur ke kanan.
- InOrder : Telusur ke kiri, print data, telusur ke kanan.
- Post Order : Telusur ke kiri, telusur ke kanan, print data.
Contoh pengkodingan push, search, pre order, in order, dan post order:
Inisialisasi
struct data{
int number;
data *left, *right;
}*root;
Push
void push(data **curr, int number){
if((*curr)==NULL){
(*curr) = (struct data *)malloc(sizeof data);
(*curr)->number=number;
(*curr)->left = (*curr)->right = NULL;
}else if(number < (*curr)->number){
push(&(*curr)->left, number);
}else if(number >= (*curr)->number){
push(&(*curr)->right, number);
}
}
Pre Order
void preOrder(data **curr){
if((*curr)!=NULL){
printf("%d -> ", (*curr)->number);
preOrder(&(*curr)->left);
preOrder(&(*curr)->right);
}
}
In Order
void inOrder(data **curr){
if((*curr)!=NULL){
inOrder(&(*curr)->left);
printf("%d -> ", (*curr)->number);
inOrder(&(*curr)->right);
}
}
Post Order
void postOrder(data **curr){
if((*curr)!=NULL){
postOrder(&(*curr)->left);
postOrder(&(*curr)->right);
printf("%d -> ", (*curr)->number);
}
}
Search
void search(data **curr, int number){
if((*curr)!=NULL){
if(number<(*curr)->number){
search(&(*curr)->left,number);
}else if(number>(*curr)->number){
search(&(*curr)->right,number);
}else{
printf("%d", (*curr)->number);
}
}else{
printf("None");
}
}
Blockchain & Hashing