Heap & Tries

Heap

Heap merupakan suatu tree-based data structure yang dimana merupakan sebuah tree yang hampir komplit yang melengkapi syarat heap property (Setiap nodepada sebuah tree yang memiliki key yang lebih besar, lebih kecil, atau sama dengan key dari parentya). Terdapat cara penentuan parent dan child pada heap, yaitu sebagai berikut:

Misalkan x adalah suatu elemen (Angka merah menandakan array)

- Parent : x / 2, cth : 4 / 2 = 2

- Left Child : x * 2, cth : 4 * 2 = 8

- Right Child : (x * 2) + 1, cth : (4 * 2) + 1 = 8 + 1 = 9

Terdapat 2 macam heap yaitu Max heap dan Min heap.

• Max Heap : Pada max heap terdapat key yang berada pada root node yang harus lebih besar daripada key anak - anaknya.

 Jika dilakukan max heap insertion:
- Node baru akan diinsert pada array index selanjutnya (Pada contoh diatas left child dari node 10)
- Akan dibandingkan node yang baru dan value node diatasnya, bila lebih besar diswap (Dilakukan sampai value parent lebih besar

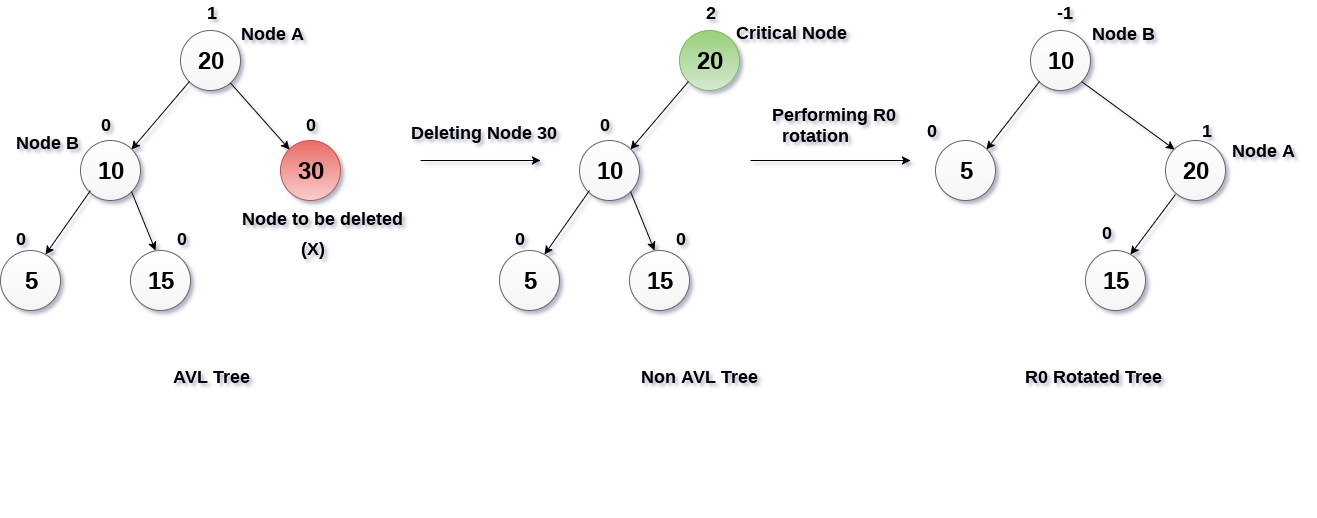
Jika dilakukan max heap deletion:
- Delete node yang ingin dihapus
- Node digantikan node yang berada di paling kanan bawah (Jika node yang dihapus memiliki left atau right child)
  - Jika heap property sudah benar maka selesai.
  - Jika value node pengganti >= node parentnya maka diswap, lalu diulang cek sampai heap property.
  - Jika tidak, tukar dengan node child paling besar.

• Min Heap : Pada min heap terdapat key yang berada pada root node yang harus merupakan nilai minimum diantara key anak - anaknya.

Min heap deletion dan insertion sama dengan max heap hanya lebih besar menjadi lebih kecil

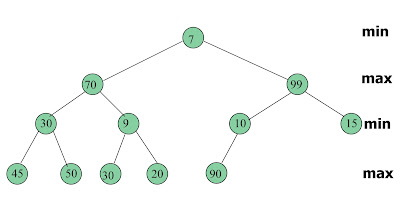
• Max-Min Heap : Merupakan binary tree komplit yang berisi level min (genap) dan max (ganjil) 

Jika dilakukan max-min heap insertion:

- Insert node baru pada index selanjutnya (Contoh diatas diinsert pada right child 10)

- Dilakukan proses heapify (Mengecek node yang baru dengan parentya dan grandparentnya sesuai dengan level)

- Proses dilakukan sampai heap property benar

Trie

Sebuah trie adalah tree mirip data structure yang menyimpan node huruf alfabet.

Insertion pada Trie
Semua karakter yang diinsert termasuk sebagai node trie individu. Children node merupakan suatu array of pointers terhadap trie node diatasnya. Karakter key merupakan index terhadap childrennya. Jika key yang diinput baru atau merupakan tambahan dari key yang sudah ada, maka diharuskan membuat node baru dari key tersebut dan tandai node selanjutnya sebagai EOW (End of Word).

Kata - kata yang terdapat pada gambar diatas adalah

- CAR

- CAB

- CAN

Aplikasi dari trie adalah

- Autocomplete 

- Search engine browser

- Bubble words

AVL Tree

 

AVL Tree berasal dari nama penemunya yaitu Adelson, Velski & Landis, yang merupakan tree yag digunakan untuk membalance binary search tree. AVL tree mengecek ketinggian dari sub-tree / leaf kiri dan kanan dan memastikan bahwa perbedaan tinggi tidak lebih dari 1. Perbedaan ini disebut Balance Factor.

Pada tree kedua dikatakan tidak balance dikarenakan sub-tree kiri dari C itu 2 dan sub-tree kanannya adalah 0, jadi perbedaan tingginya adalah 2, maka melanggar syarat balance factor. Jika masalah seperti ini terjadi, maka AVL tree mempunyai beberapa teknik untuk menyelesaikan masalah tersebut yang dinamakan AVL Rotation. 

Contoh perbaikan dari no-AVL tree ke AVL tree :

Terdapat 2 kasus dalam insertion AVL balancing yang menyebabkan diperlukannya menggunakan salah satu teknik rotasi :

Insertion

1. Single Rotation

Jika node yang menyebabkan tidak balance itu berupa kiri - kiri

Jika dilihat dari gambar diatas, T1 menyebabkan pelanggaran balance factor terhadap node z dikarenakan selisih sub-tree kiri kanan dari z adalah 2, maka untuk memperbaikinya harus dilakukan penarikan z ke kanan dan T3 menjadi sub-tree z.

2. Double Rotation

Jika node yang menyebabkan tidak balance itu berupa kiri - kanan

Jika dilihat dari gambar diatas, T3 menyebabkan pelanggaran balance factor terhadap node z dikarenakan selisih sub-tree kiri dan kanan z adalah 2, maka untuk memperbaikinya harus dilakukan penarikan y ke kiri dan T2 menjadi sub-tree y. Dikarenakan masih belum balance pada node z dilakukan rotasi sekali lagi.

Deletion

Terdapat 2 jenis kasus dalam penghapusan suatu node dalam AVL tree:

1. Jika node yang ingin dihapus merupakan node yang tidak memiliki sub-tree lalu dilakukan pengecekan kembali balance factor.

2. Jika node yang ingin dihapus memiliki sub-tree sehingga harus mencari successor atau predecessor untuk menggantikan node tersebut, lalu dilakukan pengecekan kembali balance factor.

Gambar diatas merupakan salah satu kasus yang dalam proses deletion pada suatu node yaitu kasus pertama. Maka node (30) langsung dihapus karena tidak terdapat sub-tree dan dilakukan pengecekan balance factor. Ternyata selisih sub-tree kiri dan kanan node (20) lebih dari satu. Maka node (20) ditarik ke kiri sehingga node (10) menjadi node paling awal dan node (15) berpindah menjadi sub-tree kiri node (15).

Reference ; https://algorithms.tutorialhorizon.com/avl-tree-insertion/